[最も選択された] 円錐 公式 表面積 156668-円錐 表面積 公式 小学生

円柱の表面積は 1分でわかる公式 求め方 計算 側面積 底面積との関係

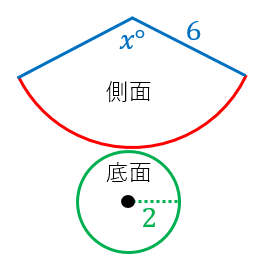
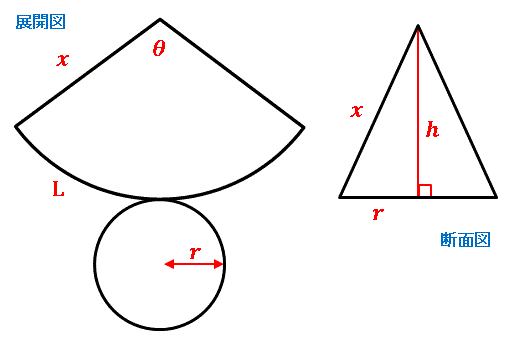
円錐に当てはめると『側面積＝ 1 2 1 2 ×弧の長さ×母線』です。 『弧の長さ＝2×底面の半径× π π 』なので、これを代入すると、『側面積＝ 1 2 1 2 ×2×底面の半径× π π ×母線＝母線×底面の半径× π π 』となります。 ちなみに『 S＝1 2lr S ＝ 1 2 l r 』についてはこちらをご覧ください。 「円」「扇形」の面積・周や弧の長さの公式 円周や円の面積、扇形の弧の長さや中学1年生 中学校数学 角柱・円柱の表面積と体積の公式 管理人 2月 5, 19 / 2月 12, 19 中学1年生で習う空間図形には、様々な立体の体積

円錐 表面積 公式 小学生

円錐 表面積 公式 小学生-半径 r、高さ h の円錐 底面の半径 r r 、母線の長さ l l 、高さ h h の円錐の表面積 S S は、次の式で求められます。 円錐の表面積 S = πr2 πrl = πr2 πr√r2 h2 S = π r 2 π r l = π r 2 π r r 2 h 2 表面積 = 半径 × 半径 × 314 半径 × 母線の長さ × 314 公式の導出方法と計算例については、「 円錐の表面積の求め方 」をご覧ください。 円錐の側面積に円錐の底面積をあわせれば、円錐の表面積ですので、 円錐の側面積＋円錐の底面積 円周率（π）×母線×底面の半径 ＋ 円周率（π）×底面の半径²

Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ The 2nd

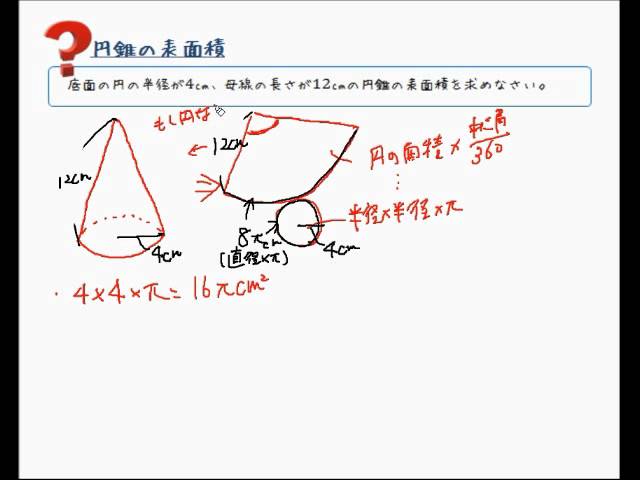
A = 面積 P ＝ 円周(近似式) 円錐 V = 体積 A = 円錐面積 r ＝ d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 ついでに、円錐の表面積の公式を証明しておきましょう。 （証明） 円錐において、底面の半径をr、母線をa、円周率をπとすると、 底面積は、 πr^2･･･① 側面積は、母線を半径とする扇形の面積だから、 πa^2×360(2πr/2πa)/360 =πa^2×2πr/2π =πar･･･② ①、②の和が表面積であるから表面積 s C i r c u l a r c o n e ( 1 ) v o l u m e V = 1 3 π r 2 h ( 2 ) l a t e r a l a r e a F = π r √ r 2 h 2 ( 3 ) s u r f a c e a r e a S = F π r 2 C i r c u l a r c o n e ( 1 ) v o l u m e V = 1 3 π r 2 h ( 2 ) l a t e r a l a r e a F = π r r 2 h 2 ( 3 ) s u r f a c e a r e a S = F π r 2

また，中心角は上の④の公式を用いると， 4 8 ×360°＝180° と求められる。 答 48∏cm2 142 次の図の円錐の体積を求めよ。 ⑴ ⑵ ⑶ ¬＝2∏r 115中学の数学幾何I_H_p0357indd 495中学の数学幾何I_H_p0357indd 49 626 PM6129 626 PM 2章 空間図形 50 144 次の図の円錐の表面積を求めよ。 ⑴ ⑵ ⑶ 146 投影図から円錐の表面積を求める方法がわかりません。 答えと解説を詳しく教えてください 問3 右の図は, 円雛の投影図です。立面図は底辺が10 cm , 等しい辺が12 cm の二等辺三角形です。このとき, 円雛の 表面積を求めなさい。ただし, 円周率はな々とします。 ゃ較 1 回答 ベストアン 中学数学円錐の表面積の求め方と公式 図 中学数学円柱の表面積の求め方・計算方法ロールケーキでわかる 中学数学円錐の高さの求め方頻出パターン コメントを残す コメントをキャンセル メールアドレスが公開されることはありません。 * が付いている欄は必須

円錐 表面積 公式 小学生のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	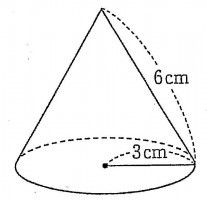円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	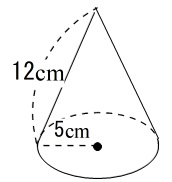円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	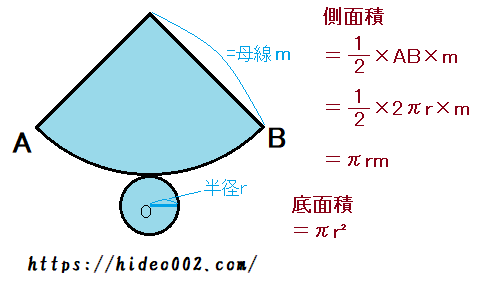円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典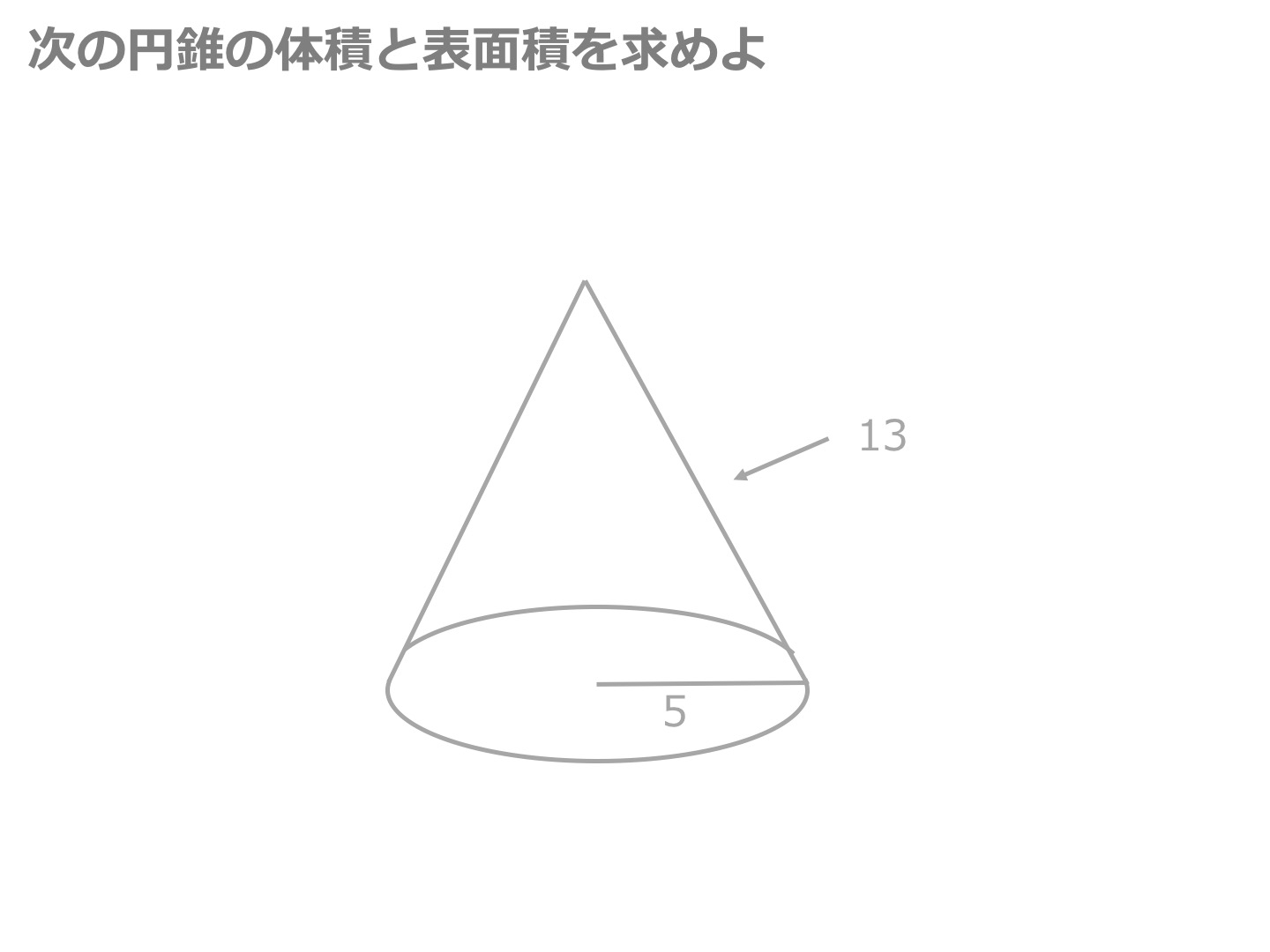
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典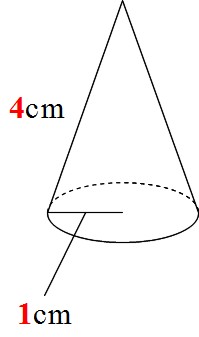
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典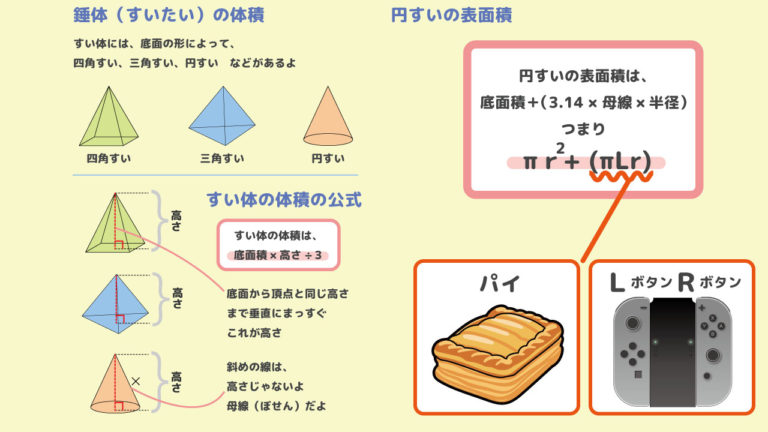
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典	円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典

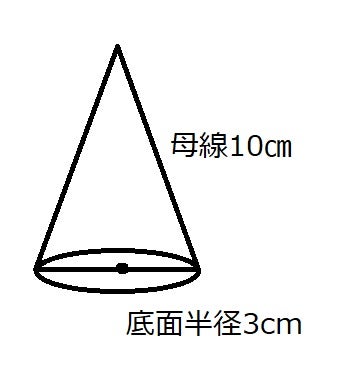
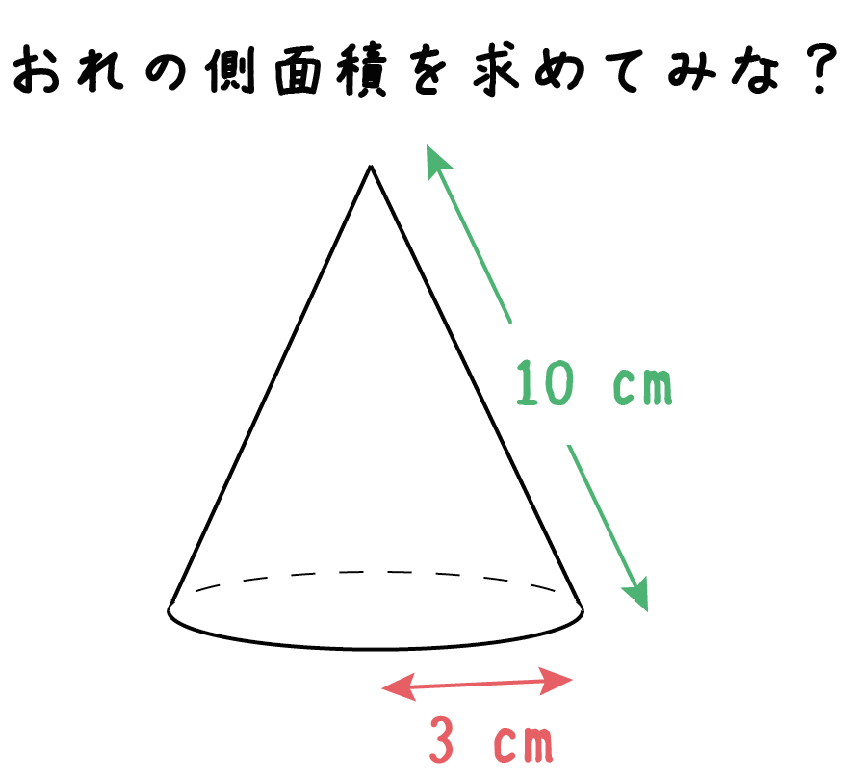
円錐の底面は円なので、底面積は$3×3×π=\textcolor{blue}{9π}$ 表面積 $\textcolor{blue}{=}$ 側面積 $\textcolor{blue}{}$ 底面積 底面積は $9π \rm cm^2$ 、側面積は $15π \rm cm^2$ よって、表面積は $15π9π=\textcolor{red}{24π\rm cm^2}$ 母線の長さ 問題図のような円錐を、Oを中心に転がすと、 $\textcolor{green}{3}$ 回転表面積を求める方法！ 母線を使った裏ワザ公式とは！？ 円錐の表面積、中心角 まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる！ こちらの関連記事はいかがでしょうか？

Incoming Term: 円錐 公式 表面積, 円錐 表面積 公式 中学, 円錐 表面積 求め方 公式, 円錐 体積 表面積 公式, 円錐 角錐 表面積 公式, 円錐 表面積 公式 母線, 円錐 表面積 公式 中学受験, 円錐 表面積 公式 小学生, 円錐 表面積 公式 簡単, 数学 円錐 表面積 公式,